11002. Tree
painting
You are given a tree (an undirected
connected acyclic graph) consisting of n vertices. You are playing a
game on this tree.
Initially, all vertices are white. On the
first turn of the game, you choose one vertex and paint it black. Then on each
turn you choose a white vertex adjacent (connected by an edge) to any black
vertex and paint it black.
Each time you choose a vertex (even during
the first turn), you gain a number of points equal to
the size of the connected component consisting only of white vertices that
contains the chosen vertex. The game ends when all vertices are painted black.
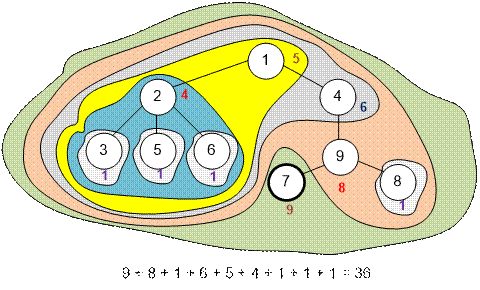
Let's see the following example:
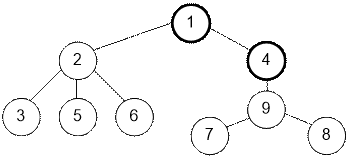
Vertices 1 and 4 are
painted black already. If you choose vertex 2, you will gain 4 points
for the connected component consisting of vertices 2, 3, 5 and 6.
If you choose vertex 9, you will gain 3 points for the connected
component consisting of vertices 7, 8 and 9.
Your task is to maximize the number of
points you gain.
Input
The first line contains an integer n (2 ≤ n ≤ 2 * 105) – the number of vertices in the
tree.
Each of the next n – 1 lines describes an edge of the tree.
Edge i is denoted by two integers ui
and vi (1 ≤ ui, vi ≤
n, ui ≠ vi), the
indices of vertices it connects.
It is guaranteed that the given edges form
a tree.
Output
Print one integer – the maximum number of
points you gain if you play optimally.
|
Sample
input 1 |
Sample
output 1 |
|
9 1 2 2 3 2 5 2 6 1 4 4 9 9 7 9 8 |
36 |
|
|
|
|
Sample
input 2 |
Sample
output 2 |
|
5 1 2 1 3 2 4 2 5 |
14 |
SOLUTION
tree
Algorithm analysis
The number of points gained is uniquely determined by the first selected vertex. It
remains to iterate through all possible vertices
as the first one, find the received number of points, and print the
maximum value among them.
Let’s start the depth-first search from the
vertex 1. Let weight[v] be the size of the subtree (number of vertices)
rooted at vertex v. Let to1, to2, …, tok be the sons of v. Then
weight[v] = 1 + weight[to1] + weight[to2] + … + weight[tok]
The second depth-first search will visit
all the vertices and recompute the maximum number of points that you can gain
if you start from this vertex.
Consider
the function dfs2. We are at the node v, which ancestor is
p. If the vertex v is chosen as the first in the game, then the
number of points obtained is s.
void dfs2(int v, int p, long long s)
Let’s make a move along the edge (v,
to) and show how to find the answer if the game is initially started
from the vertex to. In fact, we will rehang the tree from v to
node to.
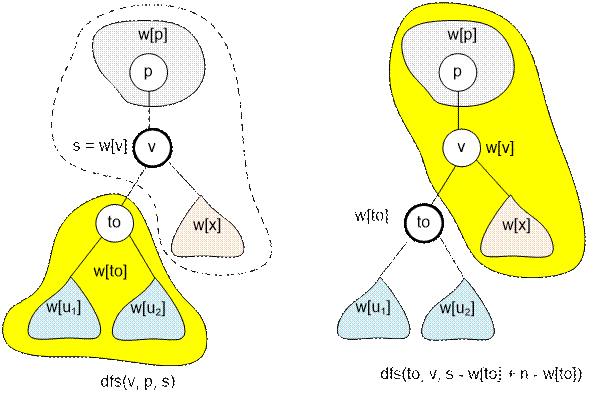
On the left, there is a tree rooted at v.
The vertex to is one of its sons, p is the ancestor. On the right,
there is a tree rooted at to.
To compute the value of weight[to] in
the right tree, subtract the weight[to] of the left tree from the value
of s in the left tree and add the number of vertices in the dotted area.
It equals n – weight[to].
Example
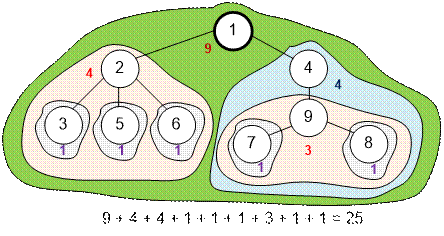
Let the first selected vertex be 1. Then the number of points
received will be 25.
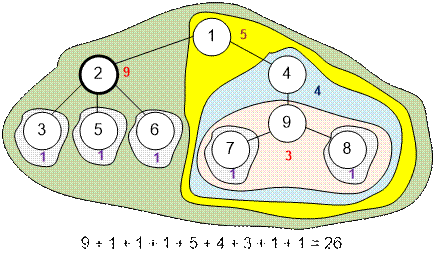
If the first selected vertex is 2, then the number of points gained is 26. The transition from vertex 1 to vertex 2 will be done
as follows. Subtract from s = 25 the value of weight[2] = 4 and add (9 – weight[4]) = 5. We get 25 – 4 + 5 = 26, the value of s for the tree rooted at node 2.
The maximum number of points is 36, which will be gained if you start the game from the vertex number 7.
Algorithm realization
Declare the adjacency list of the
graph g.
vector<vector<int>>
g;
vector<int> weight;
The function dfs1 starts a
depth-first search from a node v which parent is p. Compute weight[v]
– the size of the subtree (number of vertices) rooted at vertex v.
void dfs1(int v, int p)
{
weight[v] = 1;
for (int i = 0; i < g[v].size(); i++)
{
int to = g[v][i];
if (to == p) continue;
dfs1(to, v);
weight[v] += weight[to];
}
}
The function
dfs2 starts a depth first
search from the node v which parent is p. If the vertex v
is chosen first in the game, then the number of points gained is s.
void dfs2(int v, int p, long long s)
{
res = max(res, s);
for (int i = 0; i < g[v].size(); i++)
{
int to = g[v][i];
if (to == p) continue;
dfs2(to, v, s - weight[to] + n - weight[to]);
}
}
The main
part of the program. Read the input data. Construct a graph.
scanf("%d", &n);
g.resize(n
+ 1);
weight.resize(n
+ 1);
for (i = 1; i < n; i++)
{
scanf("%d %d", &a, &b);
g[a].push_back(b);
g[b].push_back(a);
}
Start the
depth-first search from vertex 1.
dfs1(1, 0);
Compute in
the variable s the sum of all numbers in the array weight. It equals the
number of points gained if the vertex number 1 is chosen in the game first.
s = 0;
for (i = 1; i <= n; i++)
s += weight[i];
Start the
second depth-first search from vertex 1.
dfs2(1, 0,
s);
Print the
answer.
printf("%lld\n", res);